Det kommer många frågor om hur man hanterar vinkelmått i GeoGebra och för att förstå det ordentligt bör man först sätta sig in i de olika tolkningslagren som GeoGebra använder.

I grund och botten jobbar alltid GeoGebra med radianer internt. Men de flesta användare vet inte (ännu) vad radianer är för något så det måste finnas en mekanism för att omvandla grader till radianer.

Den mekanismen heter enheter. genom att skriva ”30 deg” eller ”30°” så talar vi om för GeoGebra att vi använder grader. Vi kan också skriva till exempel ”2 rad” för att ange att vi använder radianer. Gradersymbolen kan du få genom att trycka Alt + o och ”deg” är en förkortning av engelskans ”degree”.

Så långt allt väl. Men de flesta användare skriver t.ex. ”sin(30)” när de menar ”sin(30°)” och får då oväntade resultat. Därför har utvecklarna lagt på ytterligare ett tolkningslager ovanpå de andra som används då ingen enhet explicit angetts. Det fungerar så här:

• Om argumentet är ett heltal, t.ex. 30, så tolkas det som grader
• Om argumentet är ett decimaltal, t.ex. 2.3 så tolkas det som radianer
• Om argumentet är ett symboliskt värde som inkluderar symbolen π, t.ex. π/4 så tolkas det som radianer.
• Om argumentet är ett symboliskt värde utan π, t.ex. sin(e), så tolkas det som grader.

Det här gör att 98 % av användarna får rätt första gången och känns intuitivt rimligt.

Hur fungerar de inversa trigonometriska funktionerna då? Resultatet av till exempel asin(0.5) = arcsin(0.5) bestäms av en global inställning i algebradelen av inställningarna.

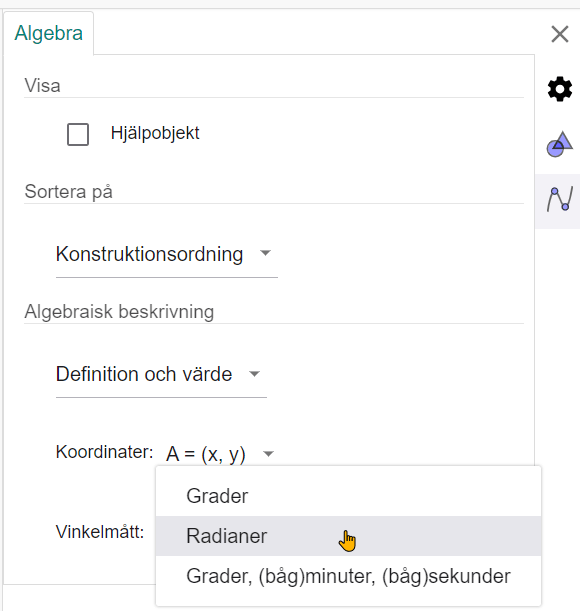
Här ser du förresten att du kan få vinklarna uttryckta som grader, (båg)minuter och (båg)sekunder.

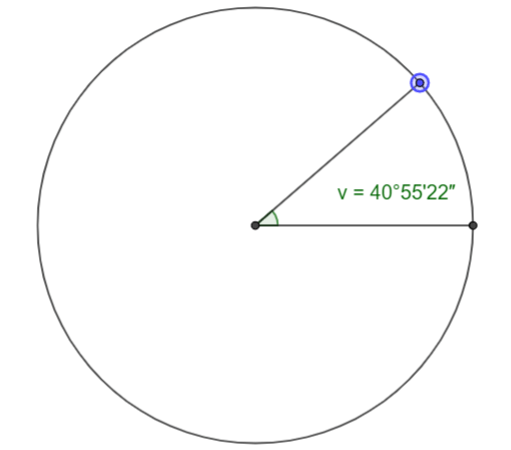
Det finns även kommandon med ett ”d” på slutet, till exempel asind(0.5), som tidigare användes för att tvinga fram svar i grader oavsett den globala inställningen. Dessa är nu underställda den globala inställningen men har behållits av kompatibilitetsskäl. De bör dock inte längre användas eller läras ut.

Är allt frid och fröjd nu? Nja, det finns alltid gränstrakter som är knepiga att navigera. Fundera till exempel på funktionen f(x) = sin(x). Vad betyder då f(90)? Det borde ju bli 1 men det blir 0,894. Det sista tolkningslagret gäller nämligen inte egendefinierade funktioner.

I alla fall inte än. Vi har kontaktat GeoGebra i Linz och uppmärksammat dem om detta. Den som hoppas på nåt gott…