Alla event, Anders Karlsson, Jonas Hall, Konferenser, Medlemmar, Svetlana Yushmanova

Praktiskt och magiskt

Lämna en kommentar

Det blir både extremt användbart och riktigt magiskt när Svetlana och Anders bygger GeoGebrakonstruktioner. Under Matematikbiennalen 2026 i Göteborg visade de fram båda sidorna och här visar vi nu upp några av konstruktionerna.

Samtliga konstruktioner de gjort kan hittas genom att söka på ”Visuell matematik”.

Om vi börjar med magin: Hur kan du trassla loss en rephärva genom att räkna med inverterade värden? Fyra personer står i en kvadrat med hörnen A, B, C och D. De håller i varsin repända två och två. Operationen Turn låter alla rotera ett kvarts varv motsols och operationen Twist låter två personer byta plats ( de som står vid position C och D). Genom att hålla koll på de matematiska motsvarigheterna till operationerna kan varje trasselhärva ges ett värde – och genom att invertera och lägga till 1 upprepade gånger kan du systematiskt – och nästan som med magi – trassla loss härvan igen. Se konstruktionen Tangles på GeoGebra.org.

Men varför nöja sig med en enda konstruktion? I den här GeoGebraboken hittar du mer än 30 olika tips, tricks, användbara genvägar, praktiska tillämpningar och fantastisk magi för dig som sett allt (och även alla andra).

Och om vi ska prata verkligt användbart även för elever så kanske några av följande är intressanta: ekvationsträning, en hel GeoGebrabok för Ma2, en till GeoGebrabok för Ma2, en för Ma3 och en för Ma4.

Hör gärna av dig om det är något du tycker saknas.

Jonas Hall, Svenska GeoGebrainstitutet

Algebraaktiviteter på svenska

Lämna en kommentar

På GeoGebras hemsida finns en stor skatt som är gömd bakom adressen geogebra.org/math. Jag har översatt tio av de högkvalitativa algebraaktiviteter som finns där till svenska. Fokus ligger på algebra och funktioner för gymnasiet.

Eftersom sidan är på engelska finns inget sätt att hitta dit från den svenska versionen av geogebra.org utan du måste knappa in hela adressen geogebra.org/math.

Sidan är väl värd ett besök. Det mesta materialet är riktat till åk 4-8 men numera finns alltså en hel del material för år 9-12 också. Jag valde att översätta några av dessa, med fokus på algebra, främst så att kunskapen om sidan geogebra.org/math sprids. Det finns en hel del fantastiska aktiviteter där och du kan (om du har ett eget gratis GeoGebrakonto) spara dina egna favoriter i en egen GeoGebrabok. Är du osäker på hur så är det bara att höra av sig.

Du kan hitta de tio översatta aktiviteterna samlade i en Geogebrabok på sidan https://www.geogebra.org/m/y4rmssst.

Det mesta kring GeoGebra kan du hitta på geogebra.se och geogebra.org. Missa inte vår Geogebra-GPT och besök gärna vårt GeoGebra-bord på Matematikbiennalen i Göteborg om du har vägarna förbi.

Alla event, Anders Karlsson, GeoGebra för lärare (2), Jonas Hall, Konferenser, Lärare och elever, Svetlana Yushmanova

För dig som sett allt

Lämna en kommentar

Från Falköping kommer återigen lite visuell och matematisk magi när duon Svetlana Yushmanova och Anders Karlsson förbereder sig för sina pass på Matematikbiennalen i Göteborg. Under rubriken För dig som sett allt har de gjort ett antal fantastiska konstruktioner. Här är några av dem.

Kartesiskt och polärt koordinatsystem samtidigt

Genom att ställa in koordinatsystemet som polärt och samtidigt skapa ett eget kartesiskt koordinatsystem med hjälp av två Talföljds-kommandon kan man visa att punkter med ”snygga” koordinater i det ena koordinatsystemet generellt får ”fula” koordinater i det andra systemet. Se konstruktionen.

Skriv innan det är för sent

En variant på ”identifiera linjens ekvation” men där linjen sakta ritas upp framför ögonen på eleverna och de måste hinna skriva ned ekvationen innan linjen ritats klart. Se konstruktionen.

Uppgift 6162 Ma2c Origo sid 275

Medellängden i en klass med 25 elever är 143 cm och standardavvikelsen är 9 cm. Tre nya elever kommer in i klassen vilket märkligt nog varken ändrar medellängden eller standardavvikelsen. Hur långa är de tre nya i klassen?

Det visar sig att lösningen går att visualisera i 3D-vyn på ett snyggt sätt. Lek själv med konstruktionen och övertyga dig om varför det stämmer och fundera på antalet lösningar. Se konstruktionen.

Hela materialet

Ovanstående är bara korta smakprov på hela GeoGebraboken som innehåller mycket mer. Missa inte deras pass på Matematikbiennalen i januari.

Alla event, Jonas Hall, Konferenser

Community Gathering

Lämna en kommentar
Dear GeoGebra Community Member,  We are excited to invite you to our upcoming GeoGebra Community Gathering to connect with us and stay updated on the latest developments. 

Date: Wednesday, July 2nd
Time: 5:00 pm to 6:00 pm (Central European Summer Time – CEST)
Location: Online via Zoom (Please register using the link below)

https://geogebra.zoom.us/meeting/register/vpBfjaUHQImV7rac2vRW4A#/registration

What to Expect:

  • 🌟 Live Demos: Experience firsthand the latest innovations from the GeoGebra Team. We’ll walk you through exciting new features and functionalities.
  • 🔍 Community Spotlight: Get an exclusive preview of inspiring projects led by members of our community.
  • ❓ Live Q&A: Have questions? We’ve got answers. Join an open Q&A session with the GeoGebra Team and Markus!

Jag hoppas kunna visa en demo av GeoGebra-GPT under det här passet.

Alla event, Jonas Hall, Konferenser

GeoGebrakonferens i Lettland 2026

Lämna en kommentar

Datumen för nästa GeoGebrakonferens är nu bestämda. Den kommer att ges i Lettland 13-15 mars 2026. 

Konferensens fokus har vidgats till att omfatta alla typer av digitala verktyg i matematikundervisningen vilket givetvis innebär att vi kommer att titta även på AI och chatbottar och hur vi kan använda dem konstruktivt så att eleverna lär sig mer, inte mindre.

Här är några konkreta förslag jag provat med viss framgång:

  1. Fota tavlan efter en genomgång. Ge fotot till en chatbot och berätta vad lektionen handlade om. Be om en pedagogisk text för de som inte var där (ev med utvidgningar) eller övningsuppgifter till nästa lektion. Tips är att skapa minitester med alternativ och då be om ”välbalanserade frågealternativ med distraktorer som tar upp vanliga feltyper”.
  2. Översätta prov till elevernas föredragna prov. Det blir inte snyggt, bilder kommer inte med, men bara textöversättningen kan hjälpa eleven.
  3. Skapa en GPT (kräver plus-konto hos ChatGPT/OpenAI) som frågar ut eleverna på ett område, kommenterar deras svar och är adaptiv (svårare/lättare frågor beroende på deras tidigare svar).
  4. Om många elever behöver hjälp och du inte hinner med – be dem fota uppgiften direkt i ChatGPT-appen för att åtminstone komma vidare. Men kräv dem också på att reflektera VAD de lärde sig och göra uppgiften själv utan hjälp igen nästa dag.
  5. För fysiklabbrapporter: Be en chatbot granska den INNAN den lämnas in och komma med en kort punktlista med förslag på vad som kan bli bättre.
Artiklar, Jonas Hall, Publikationer, Thomas Lingefjärd

Ny artikel av Thomas Lingefjärd

Lämna en kommentar

Thomas Lingefjärd har skickat in en artikel i Journal of Physical Mathematics & its Applications.

Artikeln som har titeln Motion, Velocity and Graphical Representations in GeoGebra handlar om att öka elevernas förståelse av st– och vt-grafer i fysikundervisningen. Några av slutsatserna är att:

Den övergripande uppfattningen var att GeoGebra-konstruktionerna väckte ett intresse för fysik… Ingen av studenterna uttryckte negativa åsikter om GeoGebra-demonstrationerna och laborationsaktiviteterna. Det kan vara så att de ser detta som ett modernt och träffsäkert sätt att undervisa på.

Läs hela artikeln:

motion-velocity-and-graphical-representations-in-geogebraLadda ner
Elever, GeoGebra för lärare (2), Jonas Hall, Lärare och elever, Svenska GeoGebrainstitutet

AI-assistent för GeoGebra

2 kommentarer

Jag tror faktiskt vi kan vara först i världen med att kunna erbjuda en AI-assistent som är specifikt tränad på GeoGebra och dessutom för svenska användare.

Det rör sig om en så kallad ”custom GPT”, en förpromptad version av OpenAI:s ChatGPT som har laddats med information om svenska namn på funktioner med mera. Du hittar den på http://geog.se/gpt eller http://gpthb.se/geogebra.

Du kan nu alltså få svar på hur man zoomar, konstruerar en rektangel eller hittar nollställena på en funktion oavsett plats eller tid på dygnet.

Den är inte perfekt – på samma sätt som ChatGPT i allmänhet kan den ibland göra fel och då vill jag gärna få information om det så jag kan träna den till att bli bättre.

Med det sagt så tror jag att den är bra nog för att släppas till en större publik. Det är fritt fram att låta elever använda dem också om du vill. Ju fler som testar desto bättre. Nu slipper eleverna (och kanske lärarna också) klaga på att de ”inte kan GeoGebra”.

Du måste ha ett ChatGPT-konto för att använda den, men det duger med ett gratiskonto*. Om du vill göra egna assistenter behöver du dock ett pluskonto. Om du inte vet hur man gör så hör av dig så kan jag hjälpa till.

För full transparens så går det att be den lista alla sina instruktioner samt exportera alla filer den blivit matad med.

*) Men du kan råka göra slut på hur många gånger du får ställa frågor.

Alla event, Jonas Hall, Lärare och elever, Mattecentrum, PyMa, Svenska GeoGebrainstitutet

Mattesnack med Jonas Hall

Lämna en kommentar

Hur gör man matteundervisningen mer levande, konkret – och faktiskt rolig? I ett avsnitt av Mattesnack – Mattecentrums podcast – möter vi Jonas Hall, prisad förstelärare i matematik och en av personerna bakom Svenska Geogebrainstitutet. Vi dyker ner i hur digitala verktyg som GeoGebra förändrar sättet vi lär (och lär ut) matematik – och hur modellering kan göra abstrakta begrepp begripliga.

Jonas berättar om: vad GeoGebra egentligen är – och varför det kallas ett “matematiskt laboratorium”

·      varför modellering borde få en större plats i undervisningen

·      sina böcker om matte och Python – och varför han delar allt öppet

·      varför AI, statistik och problemlösning är vägen framåt

·      hur matte kan hjälpa oss förstå världen, inte bara räkna ut den

Ett avsnitt för lärare, elever och alla som vill se matematiken från ett nytt perspektiv.

Jonas Hall, Lärare och elever, Svenska GeoGebrainstitutet

Kortlänkar

Lämna en kommentar

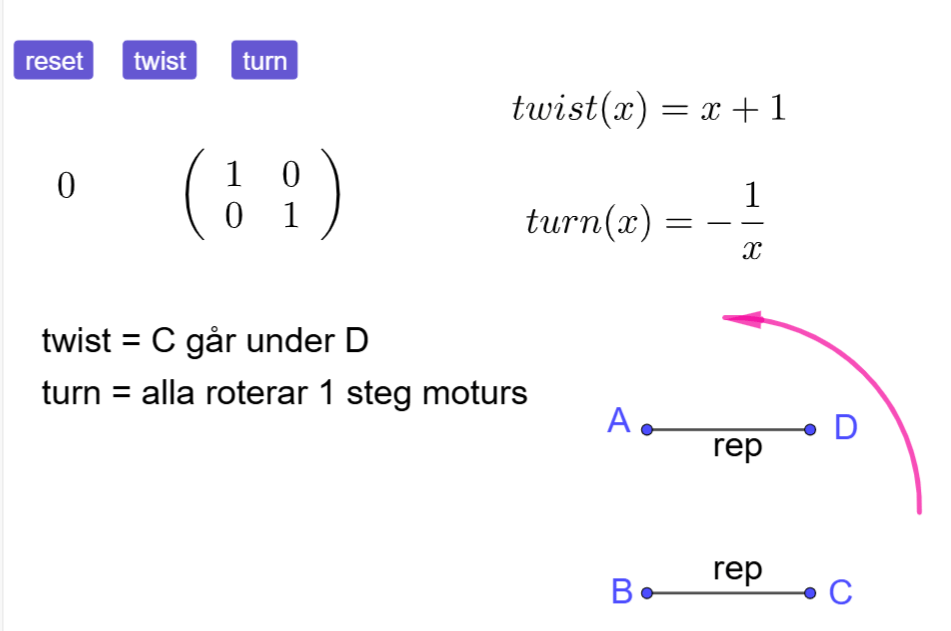
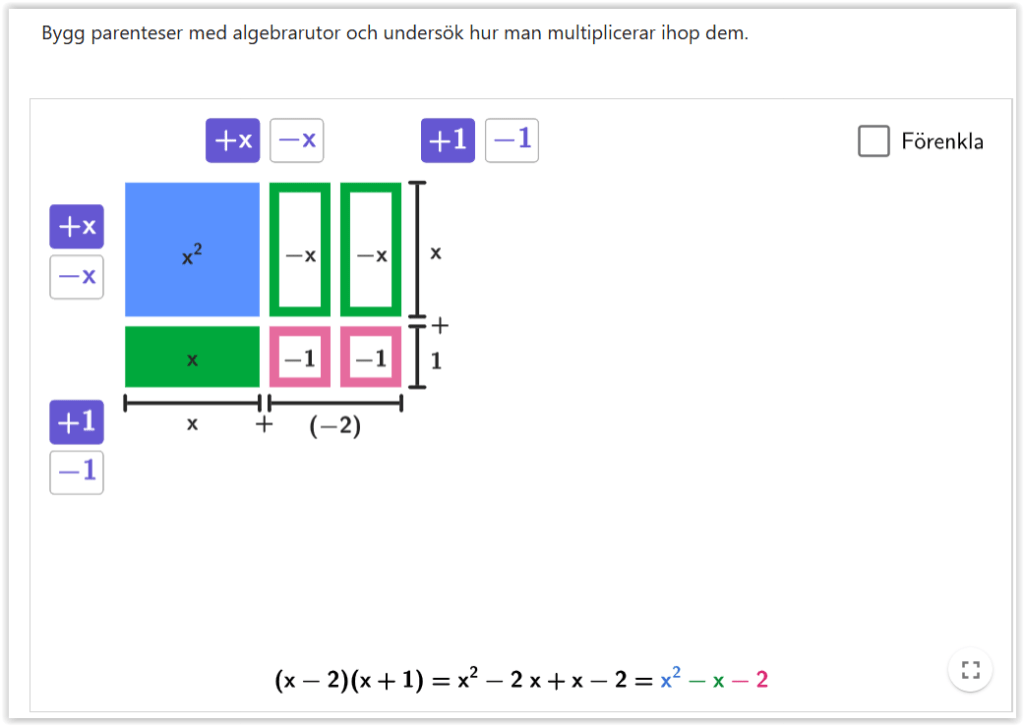
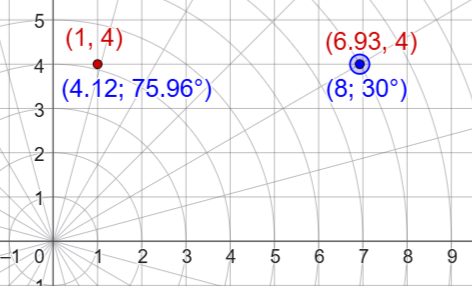
Sååå… jag gjorde en grej. Jag skaffade en domän och ett konto på https://tinyurl.com. Så nu har jag gjort kortlänkar som jag hoppas kommer till användning.

Youtube

https://geog.se/yt är den övergripande länken till vår Youtubekanal. Du kan nu enkelt ge den länken till elever och kollegor. Men jag passade också på att direktlänkar till de spellistor vi har.

https://geog.se/basics (eller /basic) och https://geog.se/grunder går till våra två spellistor som täcker grundläggande tekniker.

https://geog.se/gui (eller /ui) går till spellistan som går igenom GeoGebras grafiska gränssnitt.

https://geog.se/help (eller /support eller /download) går till spellistan som handlar om hur du laddar ned, installerar och hittar mer hjälp.

https://geog.se/online går till spellistan som handlar om hur du använder konstruktioner online, laddar ned dem, modifierar dem och laddar upp dem.

https://geog.se/np går till spellistan som visar hur du kan lösa uppgifter från frisläppta nationella prov med hjälp av GeoGebra.

https://geog.se/fy (eller /fysik) går till spellistan som visar hur du kan använda GeoGebra för fysik.

https://geog.se/konstruktioner går till spellistan som visar hur du gör några grundläggande konstruktioner.

http://geog.se/hog går till spellistan som är speciellt för högstadiet (bygger på materialet i denna mapp)

Classic

https://classic startar Classic 6 i webbläsaren.
https://classic6 går till nedladdningssidan för Classic 6 som numera tyvärr är svår att hitta.

Övrigt

https://geog.se/hem går till vår hemsida vars adress https://geogebra.se är lättare att komma ihåg än kortlänken. Men ändå.

Alla event, Jonas Hall, Svenska GeoGebrainstitutet

GeoGebra Community News

Lämna en kommentar

För nån vecka sedan var det GeoGebramöte. Här hittar du inspelningen och presentationen.

Nyheter var framför allt bättre funktionalitet i kalkylbladet för Calculator Suite samt bättre funktionalitet för tillgänglighetsverktyg och möjlighet för de som gör appar/konstruktioner att specificera tab-ordningen.

Dessutom fick vi en spontan diskussion som ledde till ett privat samtal mellan Zbynek (en av utvecklarna) och mig kring möjligheten att komma åt fysikaliska konstanter som c, G, h e med flera. Vi diskuterade att ha de ca 20-30 vanligaste konstanterna och att komma åt dem med ett kommando Const(…) eller liknande (Konstant(…) på svenska). Jag föreslog också kortformer, t.ex. att kunna skriva :e :c :G etc. Det är dock lite knepigare att implementera eftersom hela kommandotolken då behöver skrivas om, men vi kan alltid hoppas. Understreck, som i _c, skulle inte fungera då understrecket används för att skapa index i GeoGebra.

Är du intresserad av att ta igen missade community gatherings eller återbesöka tidigare sessioner? Kolla in den här aktiviteten som ger tillgång till alla tidigare presentationer och inspelningar.

Anteckna datumet för vårt nästa Community Gathering:

Nästa träff blir onsdag, 25 juni 2025 kl. 17:00. Vi meddelar detaljerna i slutet av maj.